In Shannon's paper A Mathematical Theory of Communication, he represented a communication system using the following schematic:
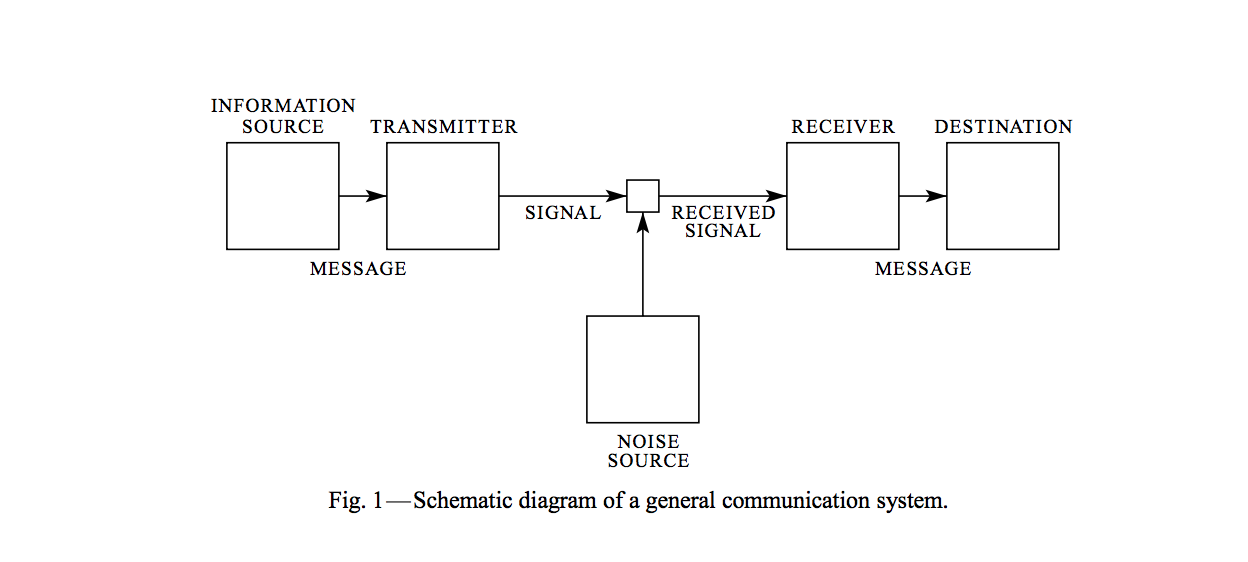
He defined Entropy, a quantity that forms the basis of information theory.
Entropy
Information Entropy is interpreted in many ways. One way that I like to think about it is in terms of " how much randomness is present in the state-space?" (Similar to Boltzmann's Entropy). It is defined as the following:
$$ H = -K \sum_{i = 1}^{n} p_i \log{p_i} $$
where $p_i$ is the probability of event i. (the constant K merely amounts to a choice of a unit of measure)
To get a feel for this, consider the following weather probabilities and their corresponding entropy:
import numpy as np
H = lambda xs: - numpy.sum(map(lambda x: x * numpy.log2(x) if x != 0 else 0, xs))
return list(map(H, [[0.25, 0.25, 0.25, 0.25], [0.5, 0.2, 0.2, 0.1], [0.8, 0.1, 0.05, 0.05], [1, 0, 0, 0]]))| Sunny | Rainy | Snowy | Foggy | Entropy |
|---|---|---|---|---|
| 0.25 | 0.25 | 0.25 | 0.25 | 2.0 |
| 0.5 | 0.2 | 0.2 | 0.1 | 1.76 |
| 0.8 | 0.1 | 0.05 | 0.05 | 1.02 |
| 1 | 0 | 0 | 0 | 0 |
As we can see, more uncertain our state-space is, the higher the entropy. If we know something for sure, there is no entropy. What's the use of this?
If you notice, we used a base of 2 for the logarithm. When the base is set to 2, we refer to the corresponding logarithm value as a bit (Shannon credits [J. W. Tukey] for this) Thus, the above Entropy can be roughly interpreted as
On avg, how many bits do we need to transmit information?
This turned out to be a useful measure for building information systems (as shown in the above figure) that send information efficiently. Every time we had to send some information, we can encode them to bits, based on the probability of each event's occurrence. Maybe, more likely an event, lesser the bits we'd want to use for it.
Now we know how many bits we need (in principle) to transmit some information, but how do we measure our system's performance? Enter cross-entropy.
Cross Entropy
$$ H(p, q) = -K \sum_{i = 1}^{n} p_i \log{q_i} $$
Where $q_i$ is our predicted probability of even $i$ and $p_i$ is the true probability of event $i$.
I think of Cross Entropy of as "How well is our system doing?". i.e "How many bits did we actually send?" (not how many do we need)
What does it mean?
Staring at this formula, we can see that if $q_i == p_i$, then cross-entropy is the same as entropy.
Relative Entropy (or KL Divergence)
The difference between Cross-Entropy and Entropy is called Relative Entropy or KL Divergence. It tells us "How close our system is to the true entropy". Higher the Relative Entropy, lesser is our efficiency.
$$ D_{KL}(p || q) = H(p, q) - H(p) $$
Thus, higher the KL divergence, higher the bit wastage.
Loss function using Cross Entropy
Cross-Entropy is often used as an error measure for Classification models. Example