Entropy as an Error Measure
Table of Contents
So Shannon dropped this absolute banger (Love the phrase Ethan!) of a paper called A Mathematical Theory of Communication, where he basically invented information theory. He drew up this neat little diagram of how communication systems work:
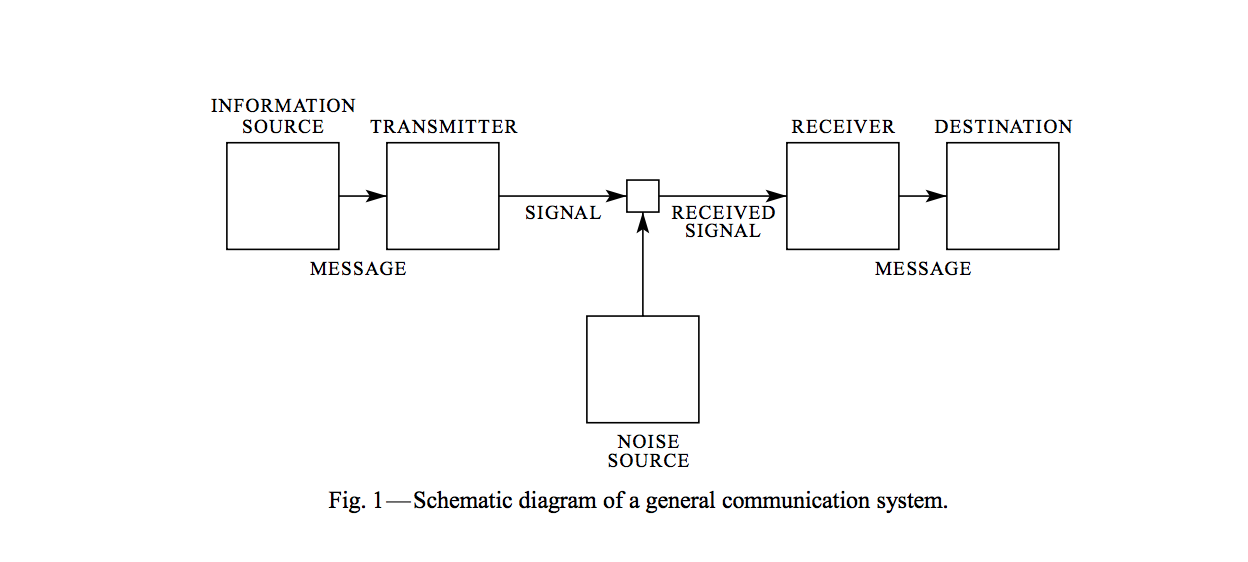
And then he went ahead and defined Entropy - this thing that became the foundation of pretty much everything we do with information.
What is Entropy Anyway?
Information Entropy gets explained in a million different ways, but here's how I like to think about it: "how much randomness is floating around in your data?" It's pretty similar to Boltzmann's Entropy from physics, if you're into that sort of thing.
The formula looks like this: $ H = -K ∑i = 1n pi log{pi} $
where \(p_i\) is the probability of event i happening. (That K constant is just there so you can pick whatever units you want - bits, nats, whatever works.)
Let me show you what this actually means with some weather data:
import numpy as np
H = lambda xs: - numpy.sum(map(lambda x: x * numpy.log2(x) if x != 0 else 0, xs))
return list(map(H, [[0.25, 0.25, 0.25, 0.25], [0.5, 0.2, 0.2, 0.1], [0.8, 0.1, 0.05, 0.05], [1, 0, 0, 0]]))
| Sunny | Rainy | Snowy | Foggy | Entropy |
|---|---|---|---|---|
| 0.25 | 0.25 | 0.25 | 0.25 | 2.0 |
| 0.5 | 0.2 | 0.2 | 0.1 | 1.76 |
| 0.8 | 0.1 | 0.05 | 0.05 | 1.02 |
| 1 | 0 | 0 | 0 | 0 |
See the pattern? The more uncertain things are, the higher the entropy. If you know something's gonna happen for sure (like that last row where it's 100% sunny), there's zero entropy. Makes sense, right?
Why Should You Care?
Notice I used base 2 for the log? When you do that, Shannon called the units bits (apparently J. W. Tukey came up with that name). So you can think of entropy as:
On average, how many bits do I need to send this information?
This turned out to be incredibly useful for building communication systems that don't waste bandwidth. The basic idea is: if something happens a lot, use fewer bits to represent it. If it's rare, you can afford to use more bits.
But here's the thing - knowing how many bits you should need is great, but how do you know if your actual system is any good? That's where cross-entropy comes in.
Cross Entropy: How Bad Are You Actually?
\[ H(p, q) = -K \sum_{i = 1}^{n} p_i \log{q_i} \]
Where \(q_i\) is what your system thinks the probability is, and \(p_i\) is what it actually is in the real world.
I think of cross-entropy as "How well is your system actually doing?" or more specifically, "How many bits are you actually using?" (as opposed to how many you theoretically need).
The cool thing is, if your system is perfect and \(q_i = p_i\) for everything, then cross-entropy equals regular entropy. Your system is as efficient as theoretically possible.
KL Divergence: The Reality Check
The difference between cross-entropy and entropy is called Relative Entropy or KL Divergence. This tells you "How far off are you from perfect?"
\[ D_{KL}(p || q) = H(p, q) - H(p) \]
Higher KL divergence means you're wasting more bits. Your system isn't as efficient as it could be.
Why Machine Learning People Love This Stuff
Cross-entropy shows up everywhere in ML as a loss function, especially for classification problems. Here's a good example if you want to dive deeper.
The intuition is pretty straightforward: if your model is confident about the right answer, cross-entropy is low. If it's confident about the wrong answer, cross-entropy goes through the roof. And if it's just confused and uncertain about everything, you get something in between.
It's basically a way to penalize both overconfidence in wrong predictions and general uncertainty, which is exactly what you want when training a classifier.